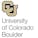This course introduces statistical inference, sampling distributions, and confidence intervals. Students will learn how to define and construct good estimators, method of moments estimation, maximum likelihood estimation, and methods of constructing confidence intervals that will extend to more general settings.


Statistical Inference for Estimation in Data Science
This course is part of Data Science Foundations: Statistical Inference Specialization
Taught in English
Some content may not be translated

Instructor: Jem Corcoran
5,864 already enrolled
Included with 
Course
(62 reviews)
Recommended experience
What you'll learn
Identify characteristics of “good” estimators and be able to compare competing estimators.
Construct sound estimators using the techniques of maximum likelihood and method of moments estimation.
Construct and interpret confidence intervals for one and two population means, one and two population proportions, and a population variance.
Details to know

Add to your LinkedIn profile
12 quizzes
Course
(62 reviews)
Recommended experience
See how employees at top companies are mastering in-demand skills

Build your subject-matter expertise
- Learn new concepts from industry experts
- Gain a foundational understanding of a subject or tool
- Develop job-relevant skills with hands-on projects
- Earn a shareable career certificate


Earn a career certificate
Add this credential to your LinkedIn profile, resume, or CV
Share it on social media and in your performance review

There are 6 modules in this course
Welcome to the course! This module contains logistical information to get you started!
What's included
1 video7 readings1 app item1 ungraded lab
In this module you will learn how to estimate parameters from a large population based only on information from a small sample. You will learn about desirable properties that can be used to help you to differentiate between good and bad estimators. We will review the concepts of expectation, variance, and covariance, and you will be introduced to a formal, yet intuitive, method of estimation known as the "method of moments".
What's included
10 videos12 readings4 quizzes1 programming assignment1 ungraded lab
In this module we will learn what a likelihood function is and the concept of maximum likelihood estimation. We will construct maximum likelihood estimators (MLEs) for one and two parameter examples and functions of parameters using the invariance property of MLEs.
What's included
5 videos6 readings2 quizzes1 programming assignment1 ungraded lab
In this module we will explore large sample properties of maximum likelihood estimators including asymptotic unbiasedness and asymptotic normality. We will learn how to compute the “Cramér–Rao lower bound” which gives us a benchmark for the smallest possible variance for an unbiased estimator.
What's included
5 videos6 readings2 quizzes1 programming assignment1 ungraded lab
In this module we learn about the theory of “interval estimation”. We will learn the definition and correct interpretation of a confidence interval and how to construct one for the mean of an unseen population based on both large and small samples. We will look at the cases where the variance is known and unknown.
What's included
5 videos6 readings2 quizzes1 programming assignment2 ungraded labs
In this module, we will generalize the lessons of Module 4 so that we can develop confidence intervals for other quantities of interest beyond the distribution mean and for other distributions entirely. This module covers two sample confidence intervals in more depth, and confidence intervals for population variances and proportions. We will also learn how to develop confidence intervals for parameters of interest in non-normal distributions.
What's included
5 videos7 readings2 quizzes1 ungraded lab
Instructor

Offered by
Recommended if you're interested in Probability and Statistics
University of Colorado Boulder

University of Colorado Boulder
University of Colorado Boulder

Google Cloud
Get a head start on your degree
This course is part of the following degree programs offered by University of Colorado Boulder. If you are admitted and enroll, your coursework can count toward your degree learning and your progress can transfer with you.
Why people choose Coursera for their career




Learner reviews
Showing 3 of 62
62 reviews
- 5 stars
54.83%
- 4 stars
20.96%
- 3 stars
6.45%
- 2 stars
9.67%
- 1 star
8.06%
New to Probability and Statistics? Start here.

Open new doors with Coursera Plus
Unlimited access to 7,000+ world-class courses, hands-on projects, and job-ready certificate programs - all included in your subscription
Advance your career with an online degree
Earn a degree from world-class universities - 100% online
Join over 3,400 global companies that choose Coursera for Business
Upskill your employees to excel in the digital economy
Frequently asked questions
Access to lectures and assignments depends on your type of enrollment. If you take a course in audit mode, you will be able to see most course materials for free. To access graded assignments and to earn a Certificate, you will need to purchase the Certificate experience, during or after your audit. If you don't see the audit option:
The course may not offer an audit option. You can try a Free Trial instead, or apply for Financial Aid.
The course may offer 'Full Course, No Certificate' instead. This option lets you see all course materials, submit required assessments, and get a final grade. This also means that you will not be able to purchase a Certificate experience.
When you enroll in the course, you get access to all of the courses in the Specialization, and you earn a certificate when you complete the work. Your electronic Certificate will be added to your Accomplishments page - from there, you can print your Certificate or add it to your LinkedIn profile. If you only want to read and view the course content, you can audit the course for free.
If you subscribed, you get a 7-day free trial during which you can cancel at no penalty. After that, we don’t give refunds, but you can cancel your subscription at any time. See our full refund policy.